Large scale document similarity search with LSH and MinHash
Large scale data comparison has become a regular need in today’s industry as data is growing by the day. Minhash and LSH are such algorithms that can compare and search similar documents in large corpus. In this post I am going to explain each individual steps of the algorithms and why they are combined and how they operate jointly to tackle the problem. First lets make it clear that we are not comparing two documents based on the semantic similarity, rather we are comparing based on word-sequence similarity (i.e. content similarity). If you want semantic similarity then there are a lot of advanced deep learning algorithms like BERT, RoBERTa, XLNet etc that can do the task for you, but here we demonstrate the process of detecting word-sequence similarity of two documents. These kinds of applications are usually useful to the News Agencies where they need to recognize that a group of articles are really all based on the same article about one particular story. Other usage could be Plagiarism detection, mirror page identification etc. Suppose you have 10K documents to compare similarity between them. This task will take O(n^2) operations (i.e. ~ 100 million operations) if you try the brute force approach - compare each document with every other document in the corpus. Clearly you need a better approach. Our problem boils down to one fact - find the near similar documents of a query document - on other words - find the nearest neighbours. LSH - locality sensitive hashing is just for this purpose. To understand how LSH solves the document comparison problem we need to dig deeper in the LSH algorithm.
Assume you are given a function get_similarity(D1, D2) which gives a similarity score between two documents - D1 and D2. Now the problem is not only you have to run the function n^2 times (given n is the number of documents) but also each function has to run a comparison of each words of a document to every other words of another document - which is m operations; given m is the number of words and both documents have m words. Clearly get_similarity(D1, D2) function itself is not efficient for large documents. The total process will cost us O(n^2*m) which is impractical for a large dataset.
LSH
Let’s start a completely different approach (fig:1) to make this whole process more efficient - instead of comparing the raw document we can compare a compressed representation of the documents.
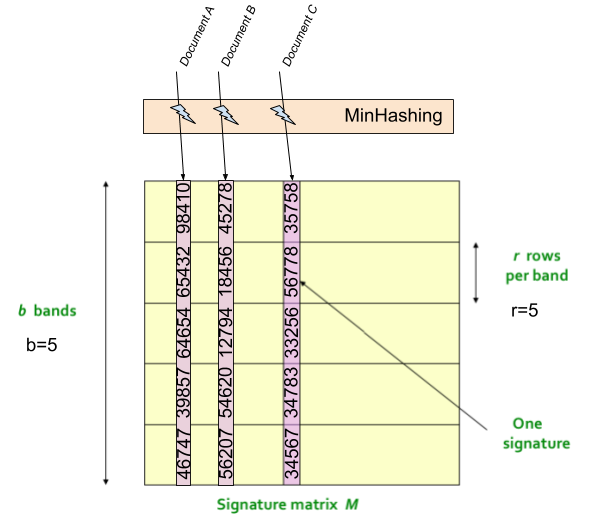
Figure-01: Signature Matrix
One approach would be we hash the documents to signatures while preserving the content-visibility of the documents through the signatures. By content-visibility I mean if you take two signatures of two similar documents and analyze, you would see a lot similarity of the signatures themselves - and for two non-similar documents you will notice a lot of dissimilarity.
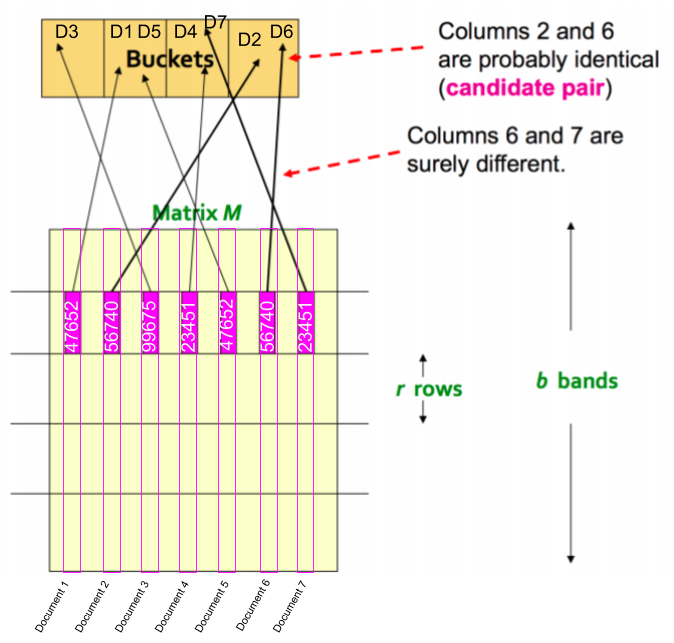
Figure-02: Distribution of the signatures over the hash buckets
Then you can divide the document signature into a number of chunks or bands. Now (fig:2) you can take a chunk (i.e. band) from a random location of a signature and compare it with a chunk (i.e. band) taken from the same location of another signature. You can map all the similar local chunks to some hash buckets - then each bucket will give you an approximate similarity of the signatures within. Hence the name LSH implies that similarity of local locations of signatures serves us a purpose. Similar signature implies similar document-content as long as the signature preserves the content-visibility through them.
Normally hash functions are very sensitive to small changes of the content - even a single bit that’s changed will completely change the hash value. While this is really what we need for exact duplicate detection but it’s actually the opposite of what we need for near duplicate detection. We need our hash function to be less sensitive to the content change so that two near similar documents are likely to produce similar signatures. A number of algorithms can do that and MinHash is one of them, which we will discuss in detail later in the article.
Now you see that the LSH algorithm eliminates the need of the get_similarity(D1, D2) function. LSH algorithm is able to do that by resolving the dimensionality problem. First we need to clear what is a curse of dimensionality in a spatial search space. Imagine in a 2D city map you are given only the longitude and not the latitude of some Gas Stations. You are dropped in some random place and you have to find the nearest Gas-Stations to you, but you can only look at the longitude of each Gas Station and your own. Now if you decide to walk towards the location that is nearest in longitude to your location, chances are you will go nearby, of course it can have a very different latitude but in general taking a step towards a close point in one-axis does really work somewhat. The more axis you use to search the more closer to exact-destination you get to go with the cost of searching each dimension individually.
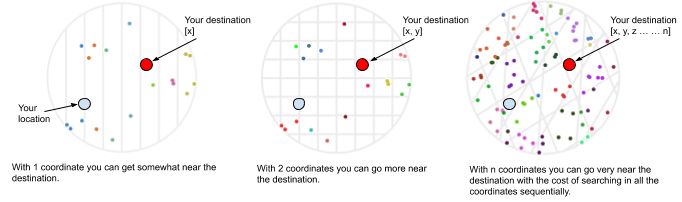
Figure-03: Curse of dimensionality in a spatial search space
Now (Fig:3) consider you have not 2D but a thousand-dimension, then looking at just one of the dimensions doesn’t really help us at all, this is because each dimension has less weight than in the previous case. We can be very near in one dimension and very far in all the others and the result is that we are really far from our destination. This is exactly why spatial indexes fail in thousand-dimension, having an “index” for each dimension doesn’t help because we have to consider all of them at the same time which is almost the same as doing a brute-force search. Now let’s relate the phenomena to our document similarity problem. Remember the get_similarity(D1, D2) function which was searching the similarity with O(m^2), this is because the two documents were searched in m dimensions, which is the same as doing brute-force search.
LSH takes a very different approach of reducing the dimensionality. The most important thing is that LSH will not give you exactly k nearest neighbors but will give you an approximation, maybe there’s a very close point that is ignored by LSH but you have to live with that.
LSH works by special-hashing (signatures of similar documents as more likely to collide) all the documents. It is trying to make a collision between documents that are “close” to each other and endup to the same bucket. Then if you have a query document, you just hash it with the same hash function and that gives you a bucket number, you go to the bucket and the documents inside that bucket are the “candidates” to be your close neighbors.
To remove the false positives you do a mini brute-force search of only those candidate documents and you find your final answer. If false-negatives are a big problem you can do this “n” times having “n” hash tables, so you go to “n” buckets to pick-up candidates instead of just one bucket, this makes you check more-documents hence more-computation but reduces the chances of missing a near neighbor. So LSH is an approximation but is very fast as you only have to check the documents inside the bucket or buckets, in general this is very close to O(1).
Now the open question is - how gonna we hash the documents to fixed-sized signatures with the tendency of being similar for similar documents?
Set Similarity with Jaccard score
There are many scales to measure the similarity between two sets - Jaccard score is one of them. It gives you a score between 0 and 1 based on the grade of similarity and this grade of similarity signifies how much two sets are overlapping each other. The amount of overlap is quantified by the intersection over union ratio i.e. The Jaccard similarity of sets A and B is |A ∩ B |/|A ∪ B. For more see here. This Jaccard score is used in many ML problems like object localization in image, document similarity search like ours and etc.
Document as a set of words
The most effective way to represent documents as sets is to construct the set of short strings that appear in the document. If we do so, then documents that share pieces as short as sentences or even phrases will have many common elements in their sets, even if those sentences appear in different orders in the two documents.

Figure-04: K-Shingling
Let’s take k words in each element of the set. If our documents are emails, picking k = 5 should be fine. If we pick k too small, then we would expect most sequences of k characters to appear in most documents and then we could have documents whose shingle-sets show high Jaccard similarity, yet the documents have none of the same sentences or even phrases. For large documents, such as research articles, choice k = 9 is considered safe.
Optional Preliminary-hashing
After k-singling a document, we can hash the elements of the set with a hash function. Thus, not only have the data been compacted, but also we can now manipulate hashed- shingles by single-word machine operations. Let’s call this a preliminary-hashing because later we’ll do a lot of other hashings. This step is optional as long as you can map the k-shingles of a document to some integers. Now we have all the documents represented as a set of hashed-shingle but they are not equal in number in every document. When document D1 is larger than document D2 then naturally D1 has a lot more hashed-shingles than D2.
MinHash - Similarity-Preserving Signature of Sets
In the previous section in LSH algorithm we had two requirements:
- The documents should have fixed-sized representations.
- Comparing these representations should give us Jaccard similarity scores.
Sets of shingles are large - even if we hash them. Our goal is to replace large sets of hashes by much smaller representations called “signatures”. It is also required that the signatures give close estimation of similarity of the sets they represent, and the larger the signatures the more accurate the estimates. The process of creating such a signature which achieves those requirements is actually the MinHash algorithm. To get a fixed-sized representation we need to start with something with a fixed number - lets start with a fixed number, say, 5 hash functions applied on every document.
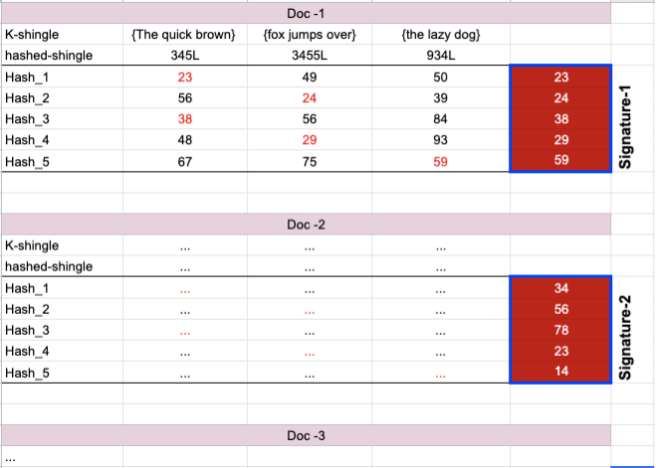
Figure-05: MinHashing process
We take a document (fig: 5) and hash it’s hashed-shingle with the first hash function Hash_1. We get 23, 49 and 50. Find the minimum hash value produced (hence the name of the algorithm is “minimum hash”) which is 23 and use it as the first component of the MinHash signature. Now take the second hash function Hash_2, and again find the minimum resulting hash value (now 24), and use this as the second component. And so on. With 5 hash functions, we’ll get the MinHash signature with 5 components - 23 24 28 29 59.
We will use the same 5 hash functions for all other documents to create the minhash signatures. Now you have the fixed-length signature for all the documents. The more hash functions you use, the longer the fingerprint you get and the higher the likelihood of duplicate documents hash collision for at least one of the components. You’re not guaranteed to get a collision, but the probability is exactly the same as the Jaccard Similarity score. Now the question remains that - where to get those 5 hashes or even more. In a simple term the definition of the function looks like this:
hash(x) = (ax + b)%c
The coefficients a and b are randomly chosen integers less than the maximum value of x. c is a prime number slightly bigger than the maximum value of x. For different choices of a and b, this hash function will produce a different random mapping of the values. So we have the ability to “generate” as many of these random hash functions as we want by just picking different values of a and b.
MinHash and LSH together
LSH is a technique of choosing the nearest neighbours - in our case choosing near similar documents. This technique is based on special hashing where the signatures can tell how far-apart or near they are from each other; based on this information LSH groups the documents to some bucket with an approximation of being similar. Thats it - LSH does nothing more than this. Now it’s our task to make those signatures and supply them to LSH. We can do this by MinHashing the documents.
Now summarising the steps together:
- Construct the set of k-shingles out of the documents.
- Optionally, hash the k-shingles to shorter numbers.
- Pick a large number of hash-functions to use for MinHash (i.e. Minhash signature length).
- Feed all the documents to the MinHash algorithm and produce document-signatures.
- Feed the signature matrix (doc. Nr. x signature-length) to the LSH algorithm.
- Get similar documents from each bucket.
- Optionally run some brute-force algorithm to check actual similarity among the documents of a bucket.
Now if you have a key document to search all similar documents to that one then you need to go through the following process:
- Construct the set of k-shingles out of the documents.
- Optionally, hash the k-shingles to shorter numbers.
- Pick the same hash functions to MinHash the key-document.
- Feed the MinHash signature to the LSH algorithm to put it in the proper bucket.
- Find all the documents in that bucket as candidates similar to the key-document.
Thus you can very fast search all the near similar documents of a key-document in almost O(n). It may not be obvious as the relationship of jaccard-similarity and the probability of candidate documents lie under some complex equations. See chapter 3 of the book Mining Massive Datasets. For the seek of evidence I’m showing a graph in figure-6. By adjusting the band b (discussed in LSH section) with different values you can get a relation between the probability-of-being-candidate-similar and jaccard-similarity score. The graph clearly shows that the more the probability of a document falls in a bucket the more jaccard-similarity it has with the other document in that bucket.
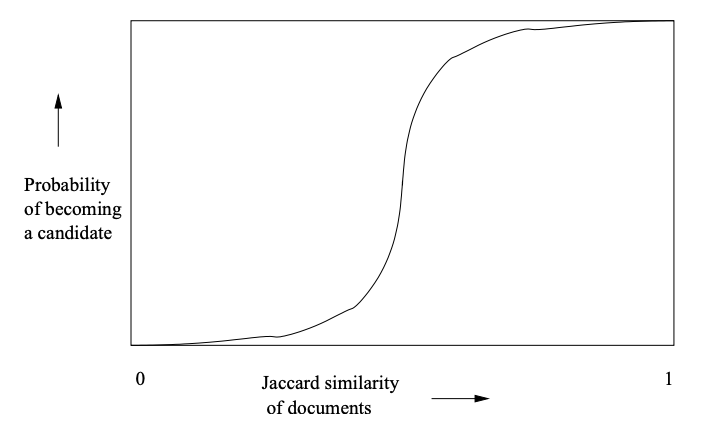
Figure-06: Relation between jaccard-score and probability for similarity of documents.
There are also other ways to measure content similarity like cosine similarity among the documents, but the Minhash-LSH algorithm will give better results. Cosine similarity does not consider word order, but, since Minhash and LSH are used on top of ngrams so it takes care of word order.
To our experience the most feasible computational solution for this project would be to use spark clusters. Here you can find nice implementation and documentation of MinHash-LSH in spark.
I am not going in details of implementation specific discussion as there are a lot of articles already there. The only thing I could not find is a clear theoretical description of all necessary steps of the MinHash-LSH algorithm, the logics behind them and how the steps are related to each other. This article is an attempt to explain them clearly. I would also like to thank all the authors of the articles mentioned in the reference as they were very helpful for me.
References
- Mining Massive Datasets, Chapter 3 - Finding Similar Items
- Fast Near-Duplicate Image Search using Locality Sensitive Hashing
- Introduction to Locality-Sensitive Hashing
- Locality sensitive hashing — LSH explained
- LSH - An effective way of reducing the dimensionality of your data
- MinHash Tutorial with Python Code
- Data Deduplication using Locality Sensitive Hashing - Matti Lyra
- LSH.9 Locality-sensitive hashing: how it works
- Quora - Answer on LSH